ResearchMy work is in computational control. Specifically, I focus on formulating problems using robust control theory and computing trajectories, controlled invariant funnels, and feedback controllers using convex and nonconvex optimization methods. The list below contains some of my work. The full list is given in my Google Scholar. |
Synthesis of trajectory, funnel, and feedback control |
|
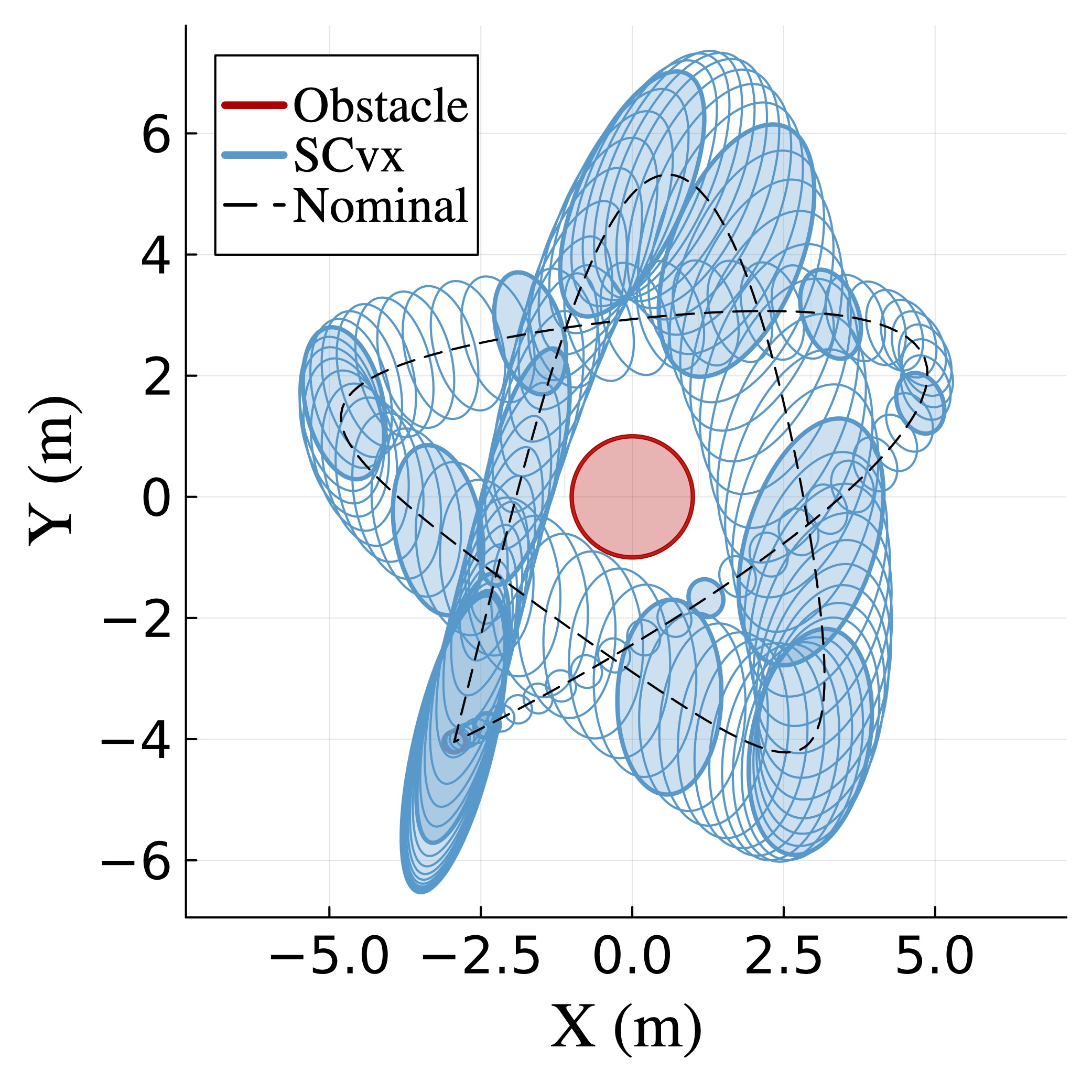
Continuous-time Constrained Funnel Synthesis for Incrementally Quadratic Nonlinear Systems
Taewan Kim, Dayou Luo, Behcet Acikmese arXiv, 2025 All about funnels. |
|
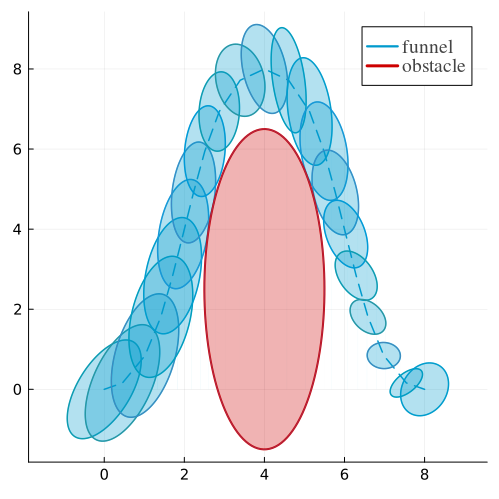
Funnel Synthesis via LMI Copositivity Conditions
Taewan Kim, Behcet Acikmese European Journal of Control, 2025 arXiv / Github Guaranteeing continuous-time invariance between discrete node points is challenging. This paper addresses the issue, and surprisingly, a matrix copositivity structure emerges. |
|
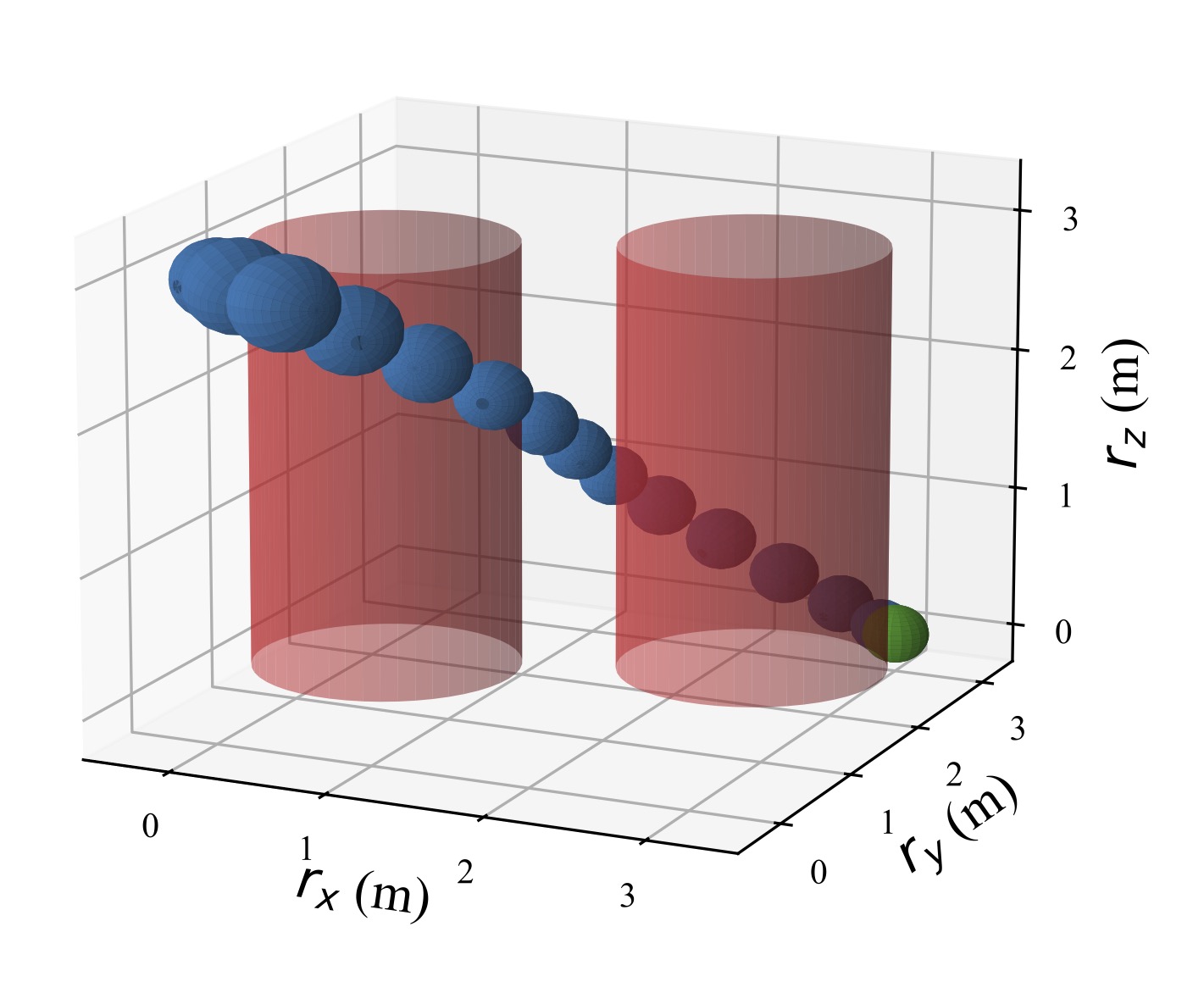
Joint Synthesis of Trajectory, Funnels, and Feedback Control
Taewan Kim, Purnanand Elango, Behcet Acikmese International Journal of Robust and Nonlinear Control, 2024 arXiv / Github Why not compute the trajectory itself as well? This paper does exactly that. |
|
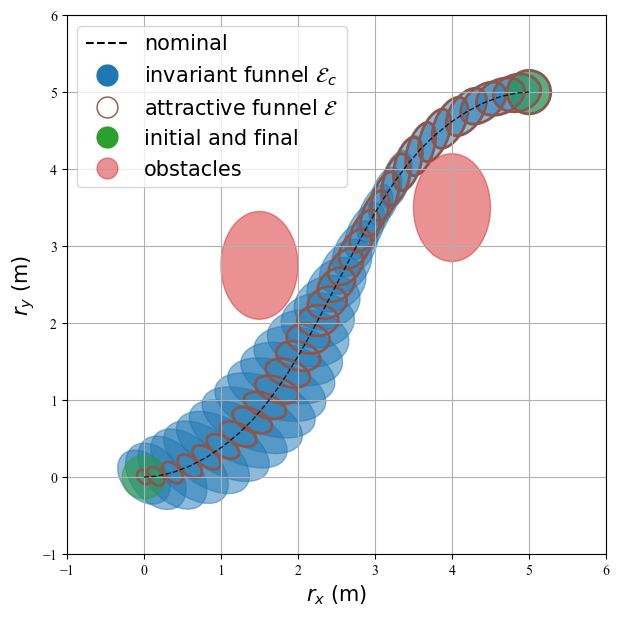
Constrained Funnel Synthesis via Numerical Optimal Control
Taewan Kim, Purnanand Elango, Taylor P. Reynolds, Behcet Acikmese, Mehran Mesbahi IEEE Control Systems Letters, 2023 arXiv / Github This reveals that funnel synthesis is essentially a trajectory optimization problem involving matrix variables. By applying numerical optimal control techniques, we can compute funnels that are less conservative compared to existing synthesis approaches. |
Application of trajectory optimization for autonomous vehicles |
|
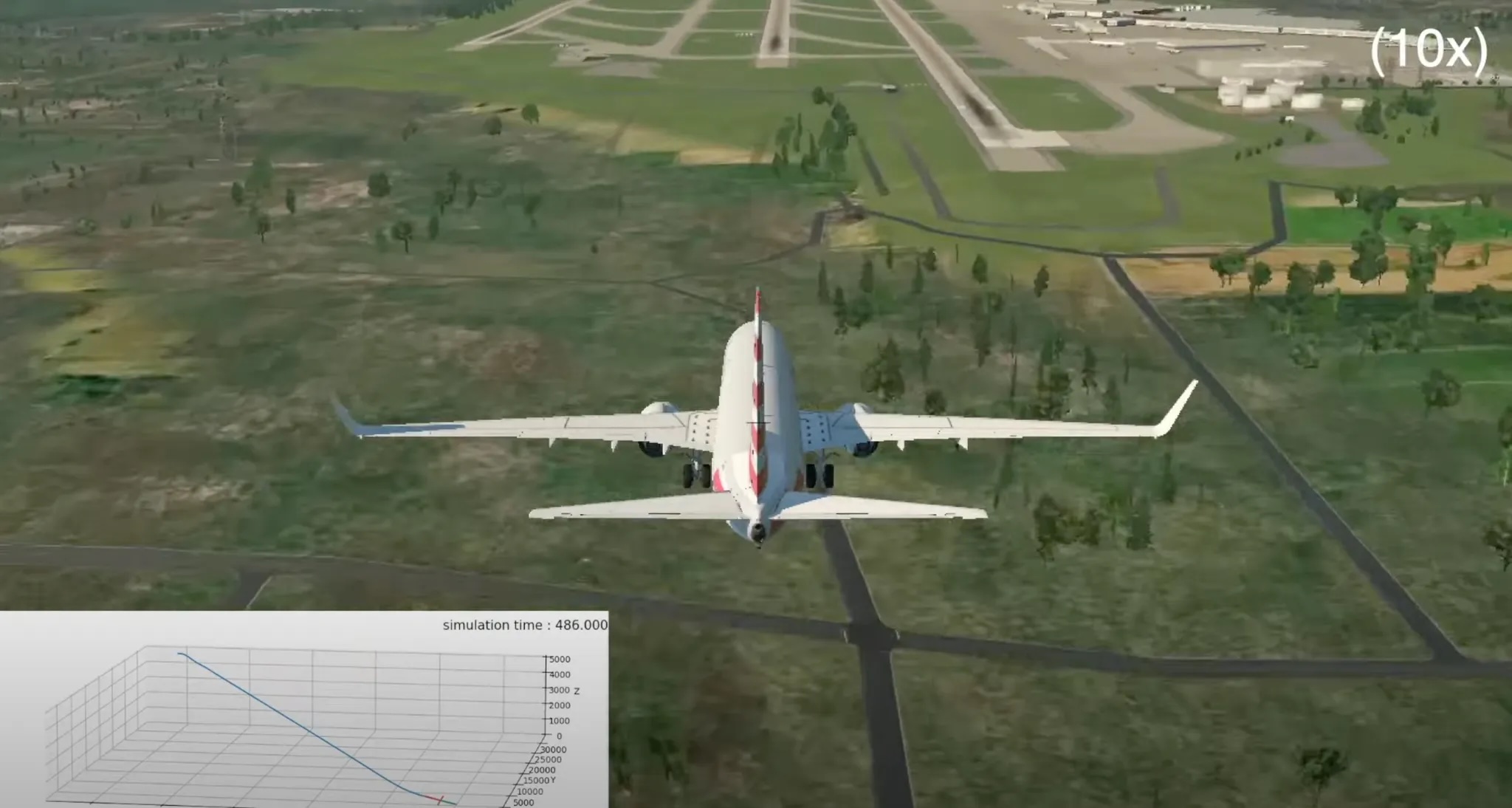
Six-Degree-of-Freedom Aircraft Landing Trajectory Planning with Runway Alignment
Taewan Kim, Abhinav G. Kamath, Niyousha Rahimi, Behcet Acikmese, Mehran Mesbahi, Jasper Corleis Journal of Guidance, Control, and Dynamics, 2025 arXiv / Video Among the many nonconvex trajectory optimization methods, here is one tailored for the 6-DoF aircraft landing problem. |
|
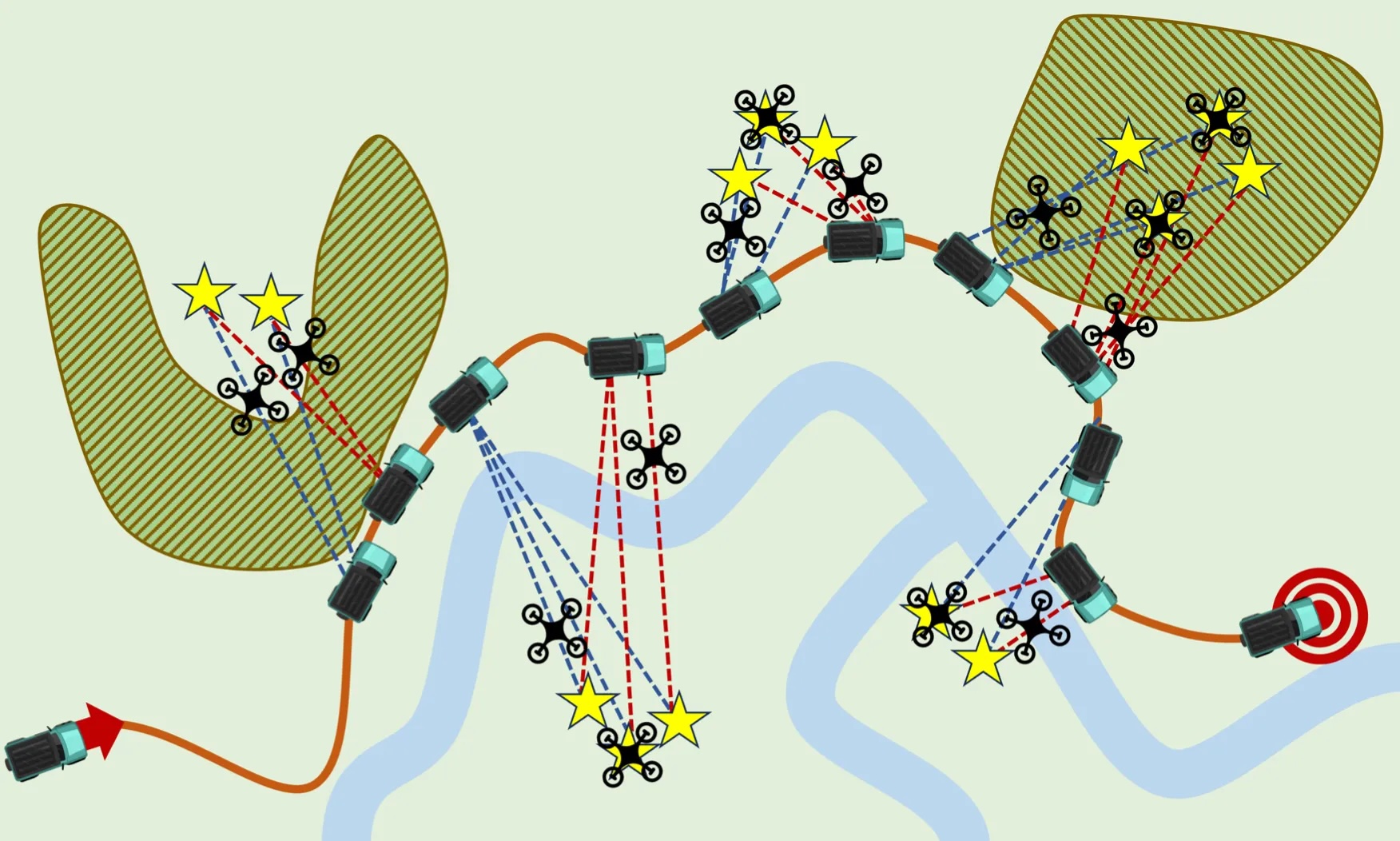
Decoupled Trajectory Planning for Monitoring UAVs and UGV Carrier by Reachable Sets
Taewan Kim, Abraham P. Vinod, Stefano Di Cairano Americal Control Conference, 2024 Paper This work addresses trajectory planning for UAVs and their UGV carrier with operational constraints, such as UAV battery limitations and coordination requirements. |
Policy Optimization Guided by Optimal Control |
|
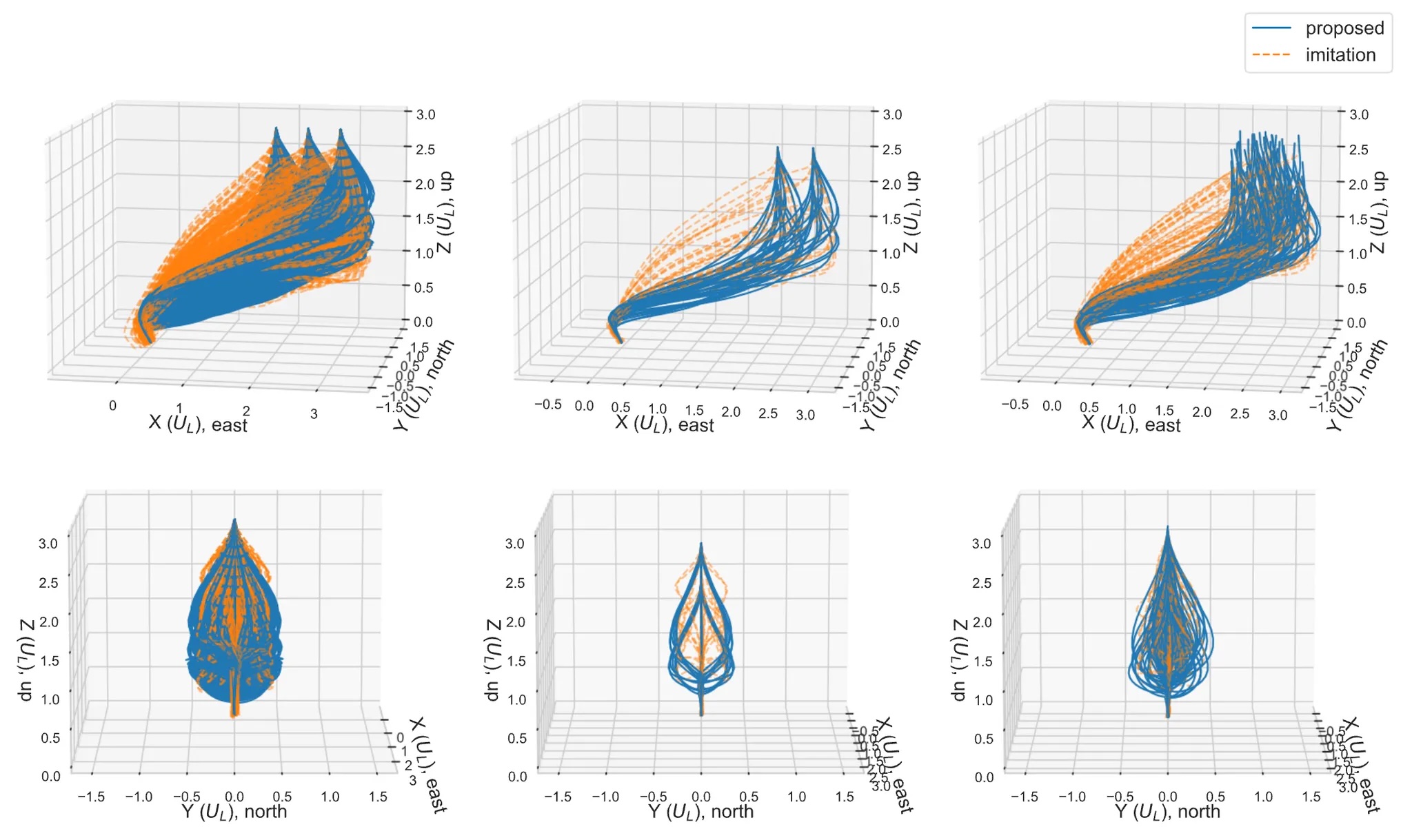
Guided Policy Search using Sequential Convex Programming for Initialization of Trajectory Optimization Algorithms
Taewan Kim, Purnanand Elango, Danylo Malyuta, Behcet Acikmese Americal Control Conference, 2022 arXiv / Video This work trains neural network policies for initializing trajectory optimization methods. The approach combines guided policy search with sequential convex programming for improved constraint satisfaction. |

|
Vision-based Target Tracking for a Skid-steer Vehicle using Guided Policy Search with Field-of-view Constraint
Taewan Kim, Chungkeun Lee, Hoseong Seo, Seungwon Choi, Wonchul Kim, H. Jin Kim International Conference on Intelligent Robots and Systems, 2018 Video Training an end-to-end policy with guided policy search for target tracking. In hindsight, I don’t think end-to-end was the most suitable approach for this task, but it was an interesting exploration. |
|
Website template from Jon Barron. |
